Best Case, Worst Case and Average Case Analysis of an Algorithm

Life can sometimes be lucky for us:

• Exams getting canceled when you are not prepared, a surprise test when you are prepared, etc. → Best case Occasionally, we may be unlucky:
• Questions you never prepared being asked in exams, or heavy rain during your sports period, etc. → Worst case However, life remains balanced overall with a mixture of these lucky and unlucky times. → Expected case

Those were the analogies between the study of cases and our everyday lives. Our fortunes fluctuate from time to time, sometimes for the better and sometimes for the worse. Similarly, a program finds it best when it is effortless for it to function. And worse otherwise.

By considering a search algorithm used to perform a sorted array search, we will analyze this feature.

Analysis of a search algorithm

Consider an array that is sorted in increasing order.

    1   7   18   28   50   180

We have to search a given number in this array and report whether it’s present in the array or not. In this case, we have two algorithms, and we will be interested in analyzing their performance separately.

1. Algorithm 1: This algorithm sequentially checks each element from the start until it finds an element that is greater than or equal to the target number.

2. Algorithm 2: This algorithm first checks if the first or last element matches the target number. If not, it finds the middle element of the array. If the middle element is greater than the target, it repeats the search in the first half; otherwise, it searches in the second half. This process of dividing the search space continues until the number is found, making it faster than the first algorithm.

Analyzing Algorithm 1: (Linear Search)

• In the best-case scenario, we might be lucky enough to find the target element as the first element of the array. In this case, we only need to make one comparison, which is a constant time operation, regardless of the array size.

  • Best case complexity = O(1)

• If we aren't so fortunate, the target element might be the last one in the array. In this case, the program would need to make 'n' comparisons, where 'n' is the number of elements in the array.

  • Worst-case complexity = O(n)

To calculate the average case time, we sum the runtimes of all possible cases and divide by the total number of cases. In this scenario, we find the average case time to be O(n). However, it's worth noting that calculating the average case time can sometimes become quite complex.

Analyzing Algorithm 2: (Binary Search)

• If we get really lucky, the first element could be the only one that gets compared. In this case, the time taken would be constant, representing O(1) time complexity.
  • Best case complexity = O(1)
• If we get unlucky, we will need to keep dividing the array into halves until we are left with a single element, meaning we exhaust the entire array.
• Hence the time taken : n + n/2 +n/4 + . . . . . . . . . . + 1 = logn with base 2
  • Worst-case complexity = O(log n)

What is log(n)

Log(n) refers to the number of times we need to divide (n) units in half until we reach a point where they can no longer be divided further.

• log8 = 3 ⇒ 8/2 + 4/2 + 2/2 → Can’t break anymore.
• log4 = 2 ⇒ 4/2 + 2/2 → Can’t break anymore.

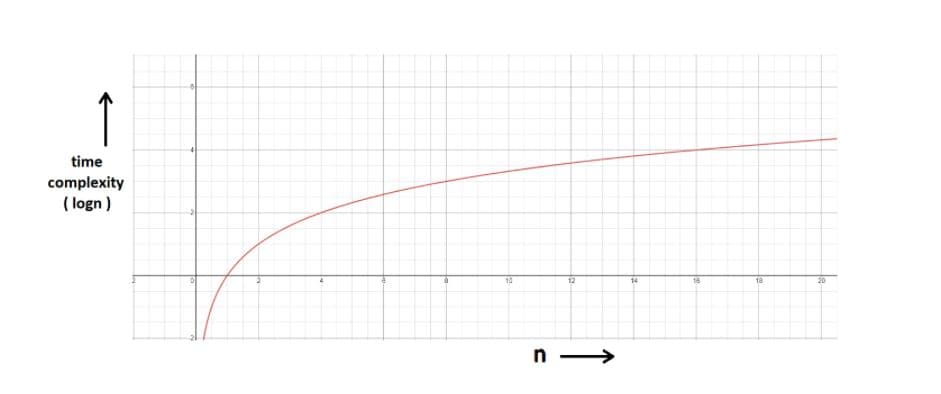
You can refer to the graph below, and you will find how slowly the time complexity (Y-axis) increases when we increase the input n (X-axis).

Space Complexity

• Time is not the only concern when analyzing algorithms; space complexity is equally important.
• For instance, creating an array of size (n) (the size of the input) results in O(n) space complexity.
• Additionally, if a function calls itself recursively (n) times, its space complexity is also O(n).

Quiz Quiz: Calculate the space complexity of a function that calculates the factorial of a given number n. Hint: Use recursion.

You might have wondered at some point why we can't calculate complexity in seconds when dealing with time complexities. Here's why:

• Not everyone’s computer is equally powerful. So we avoid handling absolute time taken. We just measure the growth of time with an increase in the input size.
• Asymptotic analysis is the measure of how time (runtime) grows with input.